D66 usability

[spank]

I was 3d printing some dice, and testing them for fairness some years ago, found that if a die is unbalanced can be made to produce relatively "fair" results if 1) re-numbered to place the deviant results at the "25%" and "75%" positions, and 2) rolled in pairs.
For a example a d6 that is twice as likely to roll a 1 or 6 as a 2,3,4 or 5 {1,1,2,3,4,5,6,6} (which is a very badly balanced die) will produce a fairly poor curve and have a fairly large deviation, 2.74 for the biased die vs 2.42 for a fair die when rolling 2d6.
But if you take the same die and number it with 2 and 5 on the sides that come up most {1,2,2,3,4,5,5,6} often you get a much smoother curve
and the deviation is only 2.35(biased) vs 2.42(fair) for a fair 1d6.

AnyDice

AnyDice is an advanced dice probability calculator, available online. It is created with roleplaying games in mind.

anydice.com

 

[bookwyrm]

I hope you calculated the standard deviation for each die range

I looked that up on Wiki, and I still don't understand...

But I learned enough to know that I didn't calculate the Standard Deviation because not only did I not know what that was, I don't really need it for what I needed to know or need to use eventually. Now, I can see the difference between using a 3 4-5 6-8 9-12 13-15 16-17 18 on 3d6 for a -3 to +3 ability modifier versus using 3 4-5 6-7 8-9 10-11 12-13 14-15 16-17 18 on 3d6 for a -5 to +5 ability modifier, and the math behind the curtains that makes the differences understandable.

On the other hand, please feel free to calculate the standard deviation for the die pairs for your own satisfaction and edification, knowledge is power!

 

[mike wightman]

Knowing the standard deviation is useful because of the 68-95-99.7 rule.

 

[bookwyrm]

Knowing the standard deviation is useful because of the 68-95-99.7 rule.

Yeah, I read that in the Wiki article (the x number +/- 7% variable for example), but I have % dice for a whole number from 1-100. Or 1d20 for 5% increments to 100.

If anyone really wants to get % values the hard way using 2dwhatever, 3dwhatever, 6dwhatever, ?dwhatever, go for it, but 2d10 is so much easier that it's kind of ridiculous to use anything else, unless you don't have access to any d10's or have a fascination for % combinations using dice other than d10's (my opinion, not trying to be mean).

The percentages for all those other combinations are great for knowing the odds of rolling something, like for random chance charts. And I'm sure there are other uses, but that's kind of beyond my needs, but it's kind of cool seeing what others can come up with, especially when it perks up my own imagination.

 

[spank]

While I understand, and agree with the sentiment, With only a few exceptions Traveller is wedded to the "d6 only" mentality. Any attempt to introduce a d4, d8 etc will likely fail. CT, MT,T4,T5,MGT,Gurps Traveller, Hero Traveller, all used D6s.
T5 says:


So anything you write to use with CT/MT/GT/T4/T5/MGT/Hero Traveller will be criticized for breaking this paradigm. Hence the D66, it still uses D66 but can be divided into different probabilities more precisely than 1d6, 2d6, 3d6, etc. It is a compromise, but one that I think would work OK for Traveller.

Believe me, I'd love to integrate other polyhedrals with Traveller, combat is one place that would really benefit from it. Take CT firearms for example, every gun from a body pistol to a rifle has the exact same damage; 3d6. I'd love to see a system where pistols are d6, PDWs are d8 and rifles are d10. Or something to that effect.

 

[kilemall]

While I understand, and agree with the sentiment, With only a few exceptions Traveller is wedded to the "d6 only" mentality. Any attempt to introduce a d4, d8 etc will likely fail. CT, MT,T4,T5,MGT,Gurps Traveller, Hero Traveller, all used D6s.
T5 says:

View attachment 6339
So anything you write to use with CT/MT/GT/T4/T5/MGT/Hero Traveller will be criticized for breaking this paradigm. Hence the D66, it still uses D66 but can be divided into different probabilities more precisely than 1d6, 2d6, 3d6, etc. It is a compromise, but one that I think would work OK for Traveller.

Believe me, I'd love to integrate other polyhedrals with Traveller, combat is one place that would really benefit from it. Take CT firearms for example, every gun from a body pistol to a rifle has the exact same damage; 3d6. I'd love to see a system where pistols are d6, PDWs are d8 and rifles are d10. Or something to that effect.

Original CT had various +1 +2 etc. Body pistol settled around 2D.

 

[Condottiere]

If you can throw more dice at a problem, you can overcome it.

 

[spank]

If you can throw more dice at a problem, you can overcome it.

LOL,

 

[spank]

Original CT had various +1 +2 etc. Body pistol settled around 2D.

CT '77 had some variations, but they were all D6 based. for example, Body pistol was 3d6-8 Autopistol was 3D-3
CT '81, TTB, and MT used 3d6 for everything from a Body pistol to a Automatic rifle,
T4 did lower the Body pistol to 2D, leave most pistols at 3D, and raise Rifles to 4D, which is a vast improvement over CT/M.
MGT had some variation, The Body pistol is 2D, the Autopistol/body pistol/snub pistol is 3D-3 and Rifles are 3D.

 

[kilemall]

CT '77 had some variations, but they were all D6 based. for example, Body pistol was 3d6-8 Autopistol was 3D-3
CT '81, TTB, and MT used 3d6 for everything from a Body pistol to a Automatic rifle,
T4 did lower the Body pistol to 2D, leave most pistols at 3D, and raise Rifles to 4D, which is a vast improvement over CT/M.
MGT had some variation, The Body pistol is 2D, the Autopistol/body pistol/snub pistol is 3D-3 and Rifles are 3D.

Umm no literally looking at book 1, 1D daggers 2D body pistol 3D most rifles with differing chances str/Dex and pen with range and armor, 4D laser carbine shotgun and broadsword, 5D for laser rifle. They are mashed together a bit, but not 3D everything.

Prefer an altered version of Striker anyway.

 

[spank]

Umm no literally looking at book 1, 1D daggers 2D body pistol 3D most rifles with differing chances str/Dex and pen with range and armor, 4D laser carbine shotgun and broadsword, 5D for laser rifle. They are mashed together a bit, but not 3D everything.

Prefer an altered version of Striker anyway.

Almost every firearm in CT is 3D, except the shotgun.

CT LLB1 '77


CT LLB1 '81

TTB/ST:

MT:

 

[spank]

Umm no literally looking at book 1, 1D daggers 2D body pistol 3D most rifles with differing chances str/Dex and pen with range and armor, 4D laser carbine shotgun and broadsword, 5D for laser rifle. They are mashed together a bit, but not 3D everything.

Prefer an altered version of Striker anyway.

I got home and pulled out my Facsimile edition, and it does list the body pistol at 2D, but everything else (except the shotgun) is 3D. So your 9mm gatomatic does the same damage as Dirty Henry's* 11mm Magnum, and Lee Harry Osgood's rifle

I'm not super up on Stiker so I'm not sure what it's damage looks like, or Snapshot for that matter.

 

[whartung]

Think they removed the damage DMs from the firearms in '77 just to simplify the game a bit?

 

[Condottiere]

Seems the logical conclusion.

I think the original intent would be to demonstrate the difference between, and effectiveness thereof, differing weapons.

 

[kilemall]

I got home and pulled out my Facsimile edition, and it does list the body pistol at 2D, but everything else (except the shotgun) is 3D. So your 9mm gatomatic does the same damage as Dirty Henry's* 11mm Magnum, and Lee Harry Osgood's rifle
View attachment 6347
I'm not super up on Stiker so I'm not sure what it's damage looks like, or Snapshot for that matter.

The distinction between the CT weapons is more in the range/armor and Dex mods, more about hit/nohit pen/nopen and handling. The body pistol for instance is harder to handle, shorter ranged, and less likely to pen so even if it is 3D in your version it’s less likely to get the job done then even the other handguns.

Striker is designed for rapid resolution of minis warfare. I like its very individualized ranges and differing pen per range. The handling Dex is listed so can be incorporated. But it does conflate the pen value with damage- higher pen, greater chance of serious/mortal wound, and does not deal well with long arms having less to hit very close/melee range vs pistols.

As I recall the facsimile edition included errata correct?

 

[aramis]

Don't recall shutters; might have gone up to 12. Was about 50 years ago, after all.

The ones my students had were 12×12 grid-style, no shutters.
Plus oral drills on them. I left the teaching profession in 2015.

 

[spank]

Was it a table they filled in? That's what I remember using. But I also remember see a little manual push button tester. It was entirely mechanical, the buttons were semi transparent, when you pushed the button in it would push against a stop with the answer written on it, and the answer show through.

Don't recall shutters; might have gone up to 12. Was about 50 years ago, after all.

The ones my students had were 12×12 grid-style, no shutters.
Plus oral drills on them. I left the teaching profession in 2015.

 

[aramis]

I looked that up on Wiki, and I still don't understand...

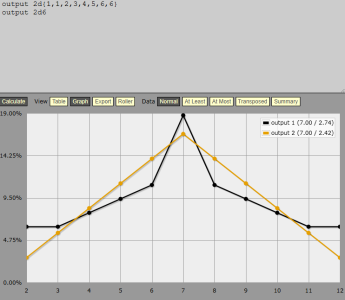
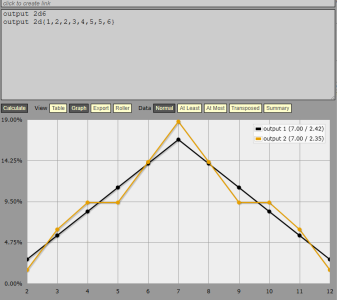
But I learned enough to know that I didn't calculate the Standard Deviation because not only did I not know what that was, I don't really need it for what I needed to know or need to use eventually. Now, I can see the difference between using a 3 4-5 6-8 9-12 13-15 16-17 18 on 3d6 for a -3 to +3 ability modifier versus using 3 4-5 6-7 8-9 10-11 12-13 14-15 16-17 18 on 3d6 for a -5 to +5 ability modifier, and the math behind the curtains that makes the differences understandable.

On the other hand, please feel free to calculate the standard deviation for the die pairs for your own satisfaction and edification, knowledge is power!

Simple way:
open MS Excel, Apple Numbers, Google Sheets, or Libre Office Spreadsheet
enter all the possibilities in a range. Let's say we put 2d6 in B2 to G7 (1-6 across, 1-6 down, cells in middle add them up - in B2, enter =B$1+$A1 then hit enter
in another cell, =stdev(B2:G7)
Note that B1:G1 is the face values on the first die
A2:A7 is the second die face values.
for 3d, unroll that content into one axis (for 2d6, it's going to be 36 entries as one axis, and the other axis is 1
for 4d, unroll the next 2d on the second axis.

The hard way: find all your permutations of outcomes (which, on 2d6 is 36 different entries, [2, 3, 3, 4, 4, 4, 5, 5, 5, 5, 6, 6, 6, 6, 6, 7, 7, 7, 7, 7, 7, 8, 8, 8, 8, 8, 9, 9, 9, 9, 10, 10, 10, 11, 11, 12]
Subtract the mean (what most call the average) from each to form a new set:
[-5, -4, -4, -3, -3, -3, -2, -2, -2, -2, -1, -1,-1,-1,-1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 4, 4, 5]
Square the members of the set
[25, 16, 16, 9, 9, 9, 4, 4, 4, 4, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 4, 4, 4, 4, 9, 9, 9, 16, 16, 25]
Sum them 210, if I calculated right.
Divide by the number of entries ... 36 in this case, giving 5.83̄3̄3̄
Squareroot that (I get 2.415...) more correctly, my calculator shows σ= 2.41522946

For another example: 1d4 and 1d6
2 3 4 5 6 7
3 4 5 6 7 8
4 5 6 7 8 9
5 6 7 8 9 10
unrolling that [2, 3, 3, 4, 4, 4, 5, 5, 5, 5, 6, 6, 6, 6, 7, 7, 7, 7, 8, 8, 8, 9. 9. 10]
Mean x̄= sum/number = 144/24 = 6
Subtracting x̄ from each gets: [-4, -3, -3, -2, -2, -2, -1, -1, -1, -1, 0, 0, 0, 0, 1, 1, 1, 1, 2, 2, 2, 3, 3, 4]
squaring each [16, 9, 9, 4, 4, 4, 1, 1, 1, 1, 0, 0, 0, 0, 1, 1, 1, 1, 4, 4, 4, 9, 9, 16]
Sum of squared array = 100
divide by 24 entries = 4.16͞66͞6
Squareroot gives σ= 2.04124145
Note that the mode is [5, 6, 7], and the median is 6.

In a proper bell curve, the standard deviation describes the points where a "normal" distribution would hit certain points... it's traditionally abbreviated with the greek lowercase sigma: σ
from the range of mean-standard_deviation to mean+standard_deviation (mean is often shown as x̄̄) is 68.27% of the total range of the sample space.
(x̄-σ ⋯ x̄+σ) ≅ 68.27%
(x̄-2σ ⋯ x̄+2σ) ≅ 95.45%
(x̄-3σ ⋯ x̄+3σ) ≅ 99.73%
it gets closer to 100% as the multiplier of sigma rises, but in non-quantized distributions, doesn't ever actually hit 100%.

Very few things are perfect to the standard distribution aka gaussian distribution, and dice rolls are NEVER actually gaussian...
A standard distribution assumes both axises to be continuous; dice are quantized, and normally represented by integers. (yes, that is an intentional pun) But 3d or more become closer and closer as to gaussian.

There are several measures of central tendency: mean, median, and mode are the major ones; standard deviation is pretty meaningless without the mean and the range. Given the two, however... it can tell you about the data. For example, 1d4+1d6 is a pretty bad fit to gaussian. Nice wide flat spot.

One fun thing I tried, once, was a once-shot of MT, but using 1d4+1d8 instead of 2d6... nice wide flat spot...played just fine.