Garnfellow
SOC-13
It's been a long time since high school geometry, but I'm not sure about T5's definitions of hexes.
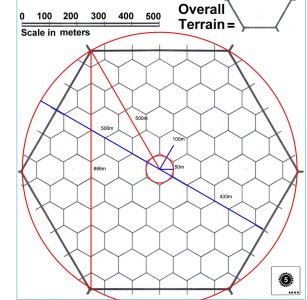
"Hex size (or hex diameter) reflects the distance from the center of a hex to the center of an adjacent similarly sized hex" (37). A World Hex is 1,000 km, a Terrain Hex is 100 km, and a Local Hex is 10 km.
Again and again, Book 3 refers to the distance across a hex as the diameter. For example, "Each Single Hex is 1 km in diameter (from the center of the Single Hex to the center of an adjacent Single Hex)" (41).
So far so good. Book 1 describes a Terrain Hex as "6,500 square km" and a Local Hex as "approximately 65 square km" (41).
But here's a diagram of hexagon
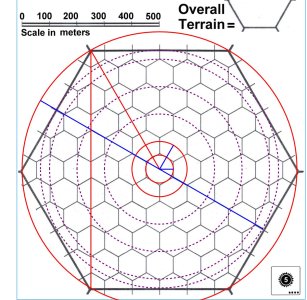
a is the length of the side, R is the circumcircle radius, d is the long diagonal (2 R), r is the apothem, and S is the short diagonal (2 r). The distance from the center of a hex to the center of an adjacent hex is not 2 R, but 2 x apothem (2 r), or S, the short diagonal.
The area of a regular hexagon is 6 x apothem squared / square root of 3. The area of a Local Hex, then, should be 6 x (10/2)^2 / square root of 3, or 87 square km. The area of a Terrain Hex 8,660 (call it 8,700 sq km), and the area of a World Hex 870,000 km.
I believe this only affects the areas in Book 1 and not anything in Book 3. Or have I completely lost it?
"Hex size (or hex diameter) reflects the distance from the center of a hex to the center of an adjacent similarly sized hex" (37). A World Hex is 1,000 km, a Terrain Hex is 100 km, and a Local Hex is 10 km.
Again and again, Book 3 refers to the distance across a hex as the diameter. For example, "Each Single Hex is 1 km in diameter (from the center of the Single Hex to the center of an adjacent Single Hex)" (41).
So far so good. Book 1 describes a Terrain Hex as "6,500 square km" and a Local Hex as "approximately 65 square km" (41).
But here's a diagram of hexagon
a is the length of the side, R is the circumcircle radius, d is the long diagonal (2 R), r is the apothem, and S is the short diagonal (2 r). The distance from the center of a hex to the center of an adjacent hex is not 2 R, but 2 x apothem (2 r), or S, the short diagonal.
The area of a regular hexagon is 6 x apothem squared / square root of 3. The area of a Local Hex, then, should be 6 x (10/2)^2 / square root of 3, or 87 square km. The area of a Terrain Hex 8,660 (call it 8,700 sq km), and the area of a World Hex 870,000 km.
I believe this only affects the areas in Book 1 and not anything in Book 3. Or have I completely lost it?
Last edited: