TheDS
SOC-13
In various games I play, there are often 4 players, and some method must be used to choose a player (such as, for who goes first). With 6 players, it's a simple matter to roll a D6 to choose. Same for 3 or 2. For 5, it's just like for 6, except you reroll a 6; as this happens only one time in six, it's not a big deal. But when you have to choose between 4 things, rolling a die and rerolling on five or six has a 1 in 3 chance of needing a reroll, which can happen multiple times in a row. So I came up with a different way to do it: use 2 dice.
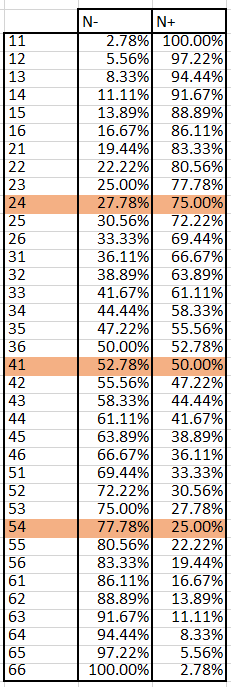
There are 36 possible combinations of 2D6, which is evenly divisible by 4, so that no rerolls are necessary. But how to divide them up in a way that you can easily remember, and doesn't require the hassle of remembering which die is the primary die (such as by doing two hi-low rolls)?
Once I figured it out, a memory aid suggested itself: 6, 5, 4, 3. You can assign those numbers to choices the same way you'd assign 1, 2, 3, 4.
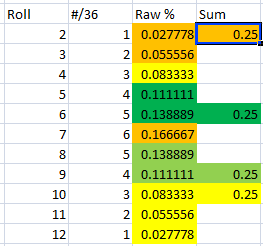
The 6 group of results is "a 6 without a 5". If either die is a 6, and the other is NOT a 5, that's choice 6.
The 5 group of results is "a 5 without a 6". If either die is a 5, and the other die is NOT a 6, that's choice 5.
Pretty simple so far, but now we have to be a little more sophisticated.
The 4 group of results is "a 5 AND 6, OR a 4 without a 5 or 6". Above, we excluded the specific combination of 5, 6, but now we need to count it to fill in for the 4s. Otherwise it works just like our previous choice: either die can be the number we care about (4), and the other cannot be a higher number.
The 3 group of results is "nothing higher than 3". This is what's left over.
Now you too can amaze your friends by making them think you've memorized a complicated table of results!
There are 36 possible combinations of 2D6, which is evenly divisible by 4, so that no rerolls are necessary. But how to divide them up in a way that you can easily remember, and doesn't require the hassle of remembering which die is the primary die (such as by doing two hi-low rolls)?
Once I figured it out, a memory aid suggested itself: 6, 5, 4, 3. You can assign those numbers to choices the same way you'd assign 1, 2, 3, 4.
The 6 group of results is "a 6 without a 5". If either die is a 6, and the other is NOT a 5, that's choice 6.
The 5 group of results is "a 5 without a 6". If either die is a 5, and the other die is NOT a 6, that's choice 5.
Pretty simple so far, but now we have to be a little more sophisticated.
The 4 group of results is "a 5 AND 6, OR a 4 without a 5 or 6". Above, we excluded the specific combination of 5, 6, but now we need to count it to fill in for the 4s. Otherwise it works just like our previous choice: either die can be the number we care about (4), and the other cannot be a higher number.
The 3 group of results is "nothing higher than 3". This is what's left over.
Now you too can amaze your friends by making them think you've memorized a complicated table of results!